Les chaînes de Markov sont un outil mathématique permettant de modéliser l’évolution d’un système dont l’état au temps t+1 ne dépend que de son état au temps t, et possédant un nombre fini d’états.
Ce document s’intéresse à l’étude de l’évolution des systèmes à partir de leur matrice de transition. En particulier, on énoncera une condition suffisante de convergence et une majoration de la vitesse de convergence dans ce cas. On s’intéressera aux cas limites où l’intervalle de temps entre deux étapes de la simulation tend vers 0, ou lorsque le nombre d’états tend vers l’infini.
Chaînes de Markov en temps discret
Généralités
Définition d’une chaîne de Markov en temps discret
Définition 1. Soit \((X_n)_{n \in \mathbb{N}}\) une famille de variables aléatoires à valeurs dans \(E\) un ensemble fini. Cette famille est une chaîne de Markov si elle vérifie la propriété de Markov : pour tout entier \(n \in \mathbb{N}^*\), pour tout couple \((y,z)\) de suites à valeurs dans E définies sur \([ 0,n-1 ]\), on a l’égalité : \[P(X_{n+1} = j | X_n=i, \forall k \in [ 0,n-1 ],\; X_k=y_k)\] \[= P(X_{n+1} = j | X_n=i, \forall k \in [ 0,n-1 ],\; X_k=z_k) \text{.}\]
On écrit alors plus simplement la probabilité de transition d’un état au suivant ainsi : \[P(X_{n+1} = j | X_n=i) \text{.}\]
Définition 2. Une chaîne de Markov est dite homogène si elle vérifie la propriété suivante : \[\forall n \in \mathbb{N},\; P(X_{n+1}=j | X_n=i) = P(X_1=j | X_0=i) \text{.}\]
Dans toute la suite, nous ne manipulerons que des chaînes homogènes.
Matrice de transition
\(E\) étant fini à n éléments, on l’identifie à \([ 1,n ]\). On définit alors naturellement une matrice à coefficients réels à partir des probabilités de transition. On exprime les coefficients de la matrice : \[\forall (i,j) \in E^2,\; p_{i,j} = P(X_1=j | X_0 = i) \text{.}\]
Remarquons que dans ce cas la matrice est stochastique ligne, c’est-à-dire que :
\[\forall i \in E,\; \sum_{j \in E} p_{i,j} = 1 \text{.}\]
Utilisation de la matrice de transition
Si \(X\) est un vecteur ligne décrivant les probabilités de se trouver dans chaque état au temps t, le vecteur ligne \(X \cdot P\) représente les probabilités de se trouver dans chaque état au temps t+1.
Probabilité de transition d’un état \(i\) à un état \(j\) en \(n\) étapes
On peut se demander s’il est possible d’itérer le processus, c’est-à-dire de déterminer la probabilité de passer d’un état \(i\) à un état \(j\) en \(n\) étapes, pour \(n \in \mathbb{N}\). On note cette probabilité : \[p^{(n)}_{i,j} = P(X_n = j | X_0 = i)\]
On note \(P^{(n)}\) la matrice des coefficients \(p^{(n)}_{i,j}\).
Théorème 1 (Chapman-Kolmogorov)
\[\forall n \in \mathbb{N}, \; P^{(n)} = P^n\]
Démonstration. Immédiat d’après \[P(X_{n+m} | X_0 = i) = \sum_{k \in E}{P(X_m=k | X_0=i) \cdot P(X_n=j | X_0=k)}\] donc \[\forall (n,m) \in \mathbb{N}^2,\; \forall (i,j) \in E^2,\; \ p^{(n+m)}{i,j} = \sum{k \in E}{p^{(m)}{i,k} \cdot p^{(n)}{k,j}} \text{.}\]
Propriétés
Remarque
L’objectif de ce document étant l’étude de \(P\) comme un endomorphisme, on cherchera ici à expliquer sous quelles conditions une chaîne de Markov converge vers un état stable, en admettant la majorité des résultats pour se concentrer sur les démonstrations algébriques qui suivent.
Définition 3. Un état est dit transient si, en partant de cet état au temps t, il existe une probabilité non nulle de ne jamais repasser par cet état. Un état non transient est dit récurrent.
Définition 4. On note \(k_i\) la période d’un état récurrent \(i\), définie par : \[k_i = \operatorname{pgcd}\{n | P(X_n=i | X_0=i) > 0\} \text{.}\]
Ainsi la période d’un état \(i\) n’est pas nécessairement la durée la plus courte au bout de laquelle on peut revenir à l’état \(i\) après l’avoir quitté. Cette définition garantit cependant que tout retour à l’état \(i\) ne peut se faire qu’après un nombre d’étapes multiple de \(k_i\). Si tout état a une période égale à 1, la chaîne est dite apériodique.
Définition 5. Si \(i\) est un état récurrent, on note \(M_i\) le temps moyen de récurrence, c’est-à-dire l’espérance du temps après lequel la chaîne reviendra en cet état, définie par : \[M_i = \sum_{n=1}^{+\infty}{n f^{(n)}_{i,i}} \text{.}\]
Notons que l’on peut avoir \(M_i=+\infty\).
Définition 6. Une chaîne de Markov est dite irréductible si pour tout couple \((i,j)\) d’états, un chemin relie les deux états dans cet ordre.
De manière équivalente, une chaîne de Markov est irréductible si et seulement si pour tout couple \((i,j)\) d’états, il existe \(k \in \mathbb{N}\) tel que \(P^k_{(i,j)} > 0\).
Mesure invariante
Définition 7. Soit \(\pi\) un vecteur ligne à coefficients dans \(\mathbb{R}\). \(\pi\) est une mesure invariante si :
- \(\forall j, 0 \leqslant \pi_j \leqslant 1\)
- \(\displaystyle\sum_{j}{\pi_j} = 1\)
- \(\forall j,\; \pi_j = \displaystyle\sum_{i}{\pi_j p_{i,j}}\)
Une mesure invariante existe si et seulement si tout état \(i\) est récurrent et \(M_i < +\infty\) (admis). Dans ce cas, \(\pi\) est unique et si on note : \[\forall j,\; v_j = \frac{1}{M_j}\] alors on a (admis) : \[\pi = \frac{v}{\|v\|}\]
Théorème 2. Si tout état est récurrent et que la chaîne est apériodique et irréductible, \(\pi\) est appelé distribution d’équilibre et on a : \[\lim_{n \rightarrow +\infty} p^{(n)}_{i,j} = \pi_j\]
Démonstration. La preuve est une conséquence du théorème de Perron-Frobenius, énoncé ci-après.
Condition suffisante de convergence
La suite des puissances de la matrice de passage \(P\) tend donc sous ces conditions (tout état est récurrent et la chaîne est apériodique et irréductible) vers une matrice dont chaque ligne est identique et égale au vecteur ligne \(\pi_j\).
Étude de la vitesse de convergence
On se place dans toute cette section dans le cas d’une chaîne irréductible et apériodique.
On note ici \(P\) la matrice stochastique colonne associée à la chaîne de Markov, soit la transposée de la matrice de transition introduite précédemment.
On suppose qu’il existe un vecteur colonne \(\pi\) stochastique vérifiant : \[\pi = P \cdot \pi \text{.}\]
\(\pi\) est donc vecteur propre de la valeur propre \(\lambda_1 = 1\).
Lemme 1. Si \(M \in \mathcal{M}_k(\mathbb{C})\) est de rayon spectral \(\rho\), alors \(\| M^n \| = O(n^{k+1} |\rho^n|)\).
Démonstration. 1er cas : \(M\) n’admet qu’une valeur propre \(\omega\).
\(M\) est semblable à \(\omega I_k + R\) avec \(R \in \mathcal{T}_k^{++}(\mathbb{C})\)
On définit \(N = M – \omega I_k\).
\(N\) a pour seule valeur propre \(0\), donc \(N\) est nilpotente.
\[\forall n \geq k,\; M^n = \sum_{i=0}^{k-1}{\binom{n}{i} \omega^{n-i} N^i}\]
\[\forall n \geq k,\; \| M^n \| \leqslant \sum_{i=0}^{k-1}{\binom{n}{i} \omega^{n-i} {\|N^i\|}} = O(n^{k+1} |\omega^n|)\]
car \(\binom{n}{i}\) est polynomial en \(n\) de degré \(i\).
2e cas : \(M\) admet \(p\) valeurs propres \(\lambda_1, \dots, \lambda_p\) distinctes 2 à 2.
On effectue la décomposition classique de \(M\) en blocs diagonaux pour se ramener au premier cas :
\[\chi_M = \prod_{i=1}^{p}{(X-\lambda_i)^{\alpha_i}}\]
\[\mathbb{R}^k = \bigoplus\limits_{i=1}^k{\text{Ker}\;(M-\lambda_i I_k)^{\alpha_i}}\]
On se ramène ainsi au premier cas en se plaçant sur M restreint à \(\text{Ker}\;(M-\lambda_i I_k)^{\alpha_i}\) pour chaque sous-espace caractéristique (possible grâce au lemme des noyaux car \(M\) stabilise tous ses sous-espaces caractéristiques).
Théorème 3 (Perron-Frobenius) Soit \(A \in \mathcal{M}_k(\mathbb{R})\) représentant une chaîne de Markov irréductible dont tout état est récurrent et apériodique.
\(1\) est valeur propre d’après ce qui précède.
On a alors \(\forall \lambda_j \in sp(A), 1=\lambda_1 > | \lambda_j |\).
De plus, soient \(\lambda_2, \dots, \lambda_k\) les autres valeurs propres de A ordonnées telles que \(\lambda_1 > | \lambda_2 | \geq | \lambda_3 | \geq \dots \geq | \lambda_k |\).
Alors, pour tout \(n \in \mathbb{N}\), \[A^n = C + O(n^{k-1} {| \lambda_2 |}^n) \text{.}\]
Démonstration. On ne démontrera ici que le second point, c’est-à-dire qu’on admettra l’existence de \(\lambda_1 = 1\) comme valeur propre de \(M\) et que cette valeur propre est de multiplicité 1.
\[\chi_A = \prod_{i=1}^k(X-\lambda_i) = (X-\lambda_1) Q(X)\]
avec
\[Q(X)=\prod_{i=2}^k(X-\lambda_i)\] et \(Q(\lambda_1) \neq 0\).
\[\mathbb{C}^k = \text{Ker}\;(A-\lambda_1 I_n) \oplus \text{Ker}\; Q(A)\] avec \(\text{Ker}\; Q(A)\) hyperplan stable par A.
\[A = Q \left( \begin{array}{c|c} \lambda_1 & (0) \\ \hline 0 & \Large\mbox{$B$} \\ [-4ex] \vdots & \\ [-0.5ex] 0 & \end{array} \right) Q^{-1}\]
avec \(Sp(B) = { \lambda_2, \dots, \lambda_r }\).
\[A^n = Q \left( \begin{array}{c|c} \lambda_1^n & 0 \dots 0 \\ \hline 0 & \Large\mbox{$B^n$} \\ [-4ex] \vdots & \\ [-0.5ex] 0 & \end{array} \right) Q^{-1} = \underbrace{ Q \left( \begin{array}{cc} \lambda_1^n & {} \\ {} & (0) \end{array} \right) Q^{-1} }_{\lambda_1^n C} + \underbrace{ Q \left( \begin{array}{c|c} 0 & 0 … 0 \\ \hline 0 & \Large\mbox{$B^n$} \\ [-4ex] \vdots & \\ [-0.5ex] 0 & \end{array} \right) Q^{-1} }_{O(n^{k-1} {| \lambda_2 |}^n)} \text{.}\]
Corrolaire 1. Sous les hypothèses du théorème ci-dessus, la mesure invariante \(\pi\) existe et est la distribution d’équilibre. On a notamment : \[C = \left( \begin{array}{c} \pi \\ \pi \\ \vdots \\ \pi \end{array} \right) \text{.}\]
File d’attente M/M/1
On étudie ici spécifiquement le cas d’une file d’attente M/M/1 limitée en temps discret.
Le terme \(M/M/1\) est issu de la notation de Kendall : Les deux M précisent la loi probabiliste régissant les arrivées et les services (ici un processus Markovien) et le 1 précise que un seul serveur traite la file.
Soit \(\mu\) un réel appelé taux d’arrivée, et \(\lambda\) une réel appelé taux de service.
Soit \(N \in \mathbb{N}\), on limite à \(N\) la longueur de la file d’attente. À chaque étape, la longueur de la file varie au maximum de 1. La probabilité que la file s’allonge est \(0 < \mu < 0.5\), et la probabilité que la file se raccourcisse est \(\mu < \lambda < 1-\mu\). Si la file est vide (état 0), elle ne peut pas se raccourcir et si la file est pleine (état \(N-1\)), elle ne peut pas s’allonger.
Le processus ainsi décrit est représenté par la matrice stochastique ligne \(P\) suivante :
\[P = \left( \begin{array}{ccccc} 1-\mu & \mu & {} & {} & (0) \\ \lambda & (1-\lambda-\mu) & \mu & {} & {} \\ {} & \ddots & \ddots & \ddots & {} \\ {} & {} & \ddots & \ddots & \ddots \\ {} & {} & \lambda & (1-\lambda-\mu) & \mu \\ (0) & {} & {} & \lambda & 1-\lambda \\ \end{array} \right)\]
Vitesse de convergence
Théorème 4 : Perron-Frobenius amélioré
\[\forall n \in \mathbb{N}, \; \|P^n – \lim\limits_{k \rightarrow +\infty} P^k\| = |\omega_2|^n\] pour une certaine norme ne dépendant que de P, où \(\omega_2\) est la plus grande valeur propre en valeur absolue de \(P\) telle que \(| \omega_2 | < 1\).
Démonstration. Soit \[D = \left(\begin{array}{ccccc} 1 & {} & {} & {} & (0) \\ {} & \frac{\mu}{\lambda} & {} & {} & {} \\ {} & {} & \frac{\mu^2}{\lambda^2} & {} & {} \\ {} & {} & {} & \ddots & {} \\ (0) & {} & {} & {} & \frac{\mu^{n-1}}{\lambda^{n-1}} \end{array} \right)\]
On a \(D \in S_n^{++}(\mathbb{R})\).
Soit \(S = D P\) donc \(P = D^{-1} S\)
Un calcul matriciel par récurrence donne \(S \in S_n(\mathbb{R})\), c’est-à-dire \(S\) symétrique.
On définit le produit scalaire : \(<\cdot,\cdot> : (X,Y) \rightarrowtail {}^t \! X D Y\) et \(f : X \rightarrowtail P X\).
On a alors :
\[\begin{aligned} <f(Y),X> &= {}^t \! (P Y) D X \\ {} &= {}^t \! Y {}^t \! (D^{-1} S) D X \\ {} &= {}^t \! Y S D^{-1} D X \\ {} &= {}^t \! Y S X \\ {} &= <Y,f(X)> \text{.}\end{aligned}\]
\(f\) est donc symétrique pour \(<\cdot,\cdot>\).
Soit \(B\) une base orthonormée pour \(<\cdot,\cdot>\), il existe \(Q \in GL_n(\mathbb{R})\) telle que \(P = Q P’ Q^{-1}\) où \(P’\) est la matrice de f dans \(B\), et Q la matrice de changement de base correspondante.
On a alors \(P’\) symétrique réelle donc diagonalisable, d’où il existe
\(R \in GL_n(\mathbb{R})\) telle que \(P’ = R P” R^{-1}\) avec \(P”\) réelle diagonale.Ainsi \(P = Q R P” R^{-1} Q^{-1}\)
Quitte à permuter les colonnes de \(R\), on peut supposer que \(P”\) est de la forme \(Diag(\lambda_1,\lambda_2,\dotsc, \lambda_N)\) avec \(|\lambda_1| \leqslant \dotsc \leqslant |\lambda_N|\).
D’après les résultats admis de la première section, \(1\) est valeur propre à gauche de \(P\), et on admet
\(1 \leqslant |\lambda_2| \leqslant \dotsc \leqslant |\lambda_N|\).Soit \(p \in [ 1 , N-1 ]\) tel que \(\lambda_1 = |\lambda_2| = \dotsc = |\lambda_p| = 1\) et \(|\lambda_{p+1}| \neq 1\)
Soit \(H = Q R\) et \(n \in \mathbb{N}\). \[P^n = H P”^{n} H^{-1} = H \mathrm{Diag}(\pm 1, \pm 1, \dotsc, \pm 1, \lambda_{p+1}^n, \dotsc, \lambda_N^n) H^{-1}\]
Ainsi, en posant la norme \(\| \cdot \| : M \rightarrowtail \|H^{-1} M H\|_{\infty}\), on a : \[\forall n \in \mathbb{N}, \|P^n – H \mathrm{Diag}(\pm 1, \pm 1, \dotsc, \pm 1, 0, \dotsc, 0) H^{-1} \| = |\lambda_{p+1}|^n \text{.}\]
Calcul des valeurs propres de P
On admet le théorème donné par l’article [9] qui nous donne les valeurs propres explicites de la matrice de transition :
Théorème 5
\[\operatorname{sp}(P) = \left\lbrace 2 \sqrt{\lambda \mu} \cos(\frac{k \pi}{N})+1-\lambda-\mu | k \in [ 1,N-1 ] \right\rbrace \cup \left\lbrace 1 \right\rbrace\]
Ainsi on a :
Corrolaire 2
\[\omega_2 = 2 \sqrt{\lambda \mu} \cos\left(\frac{\pi}{N}\right)+1-\lambda-\mu\]
Cette valeur de \(\omega_2\) va nous permettre de contrôler la convergence de la file d’attente vers sa distribution d’équilibre.
Application : Convergence vers une distribution d’équilibre pour une file non limitée
Vitesse de convergence
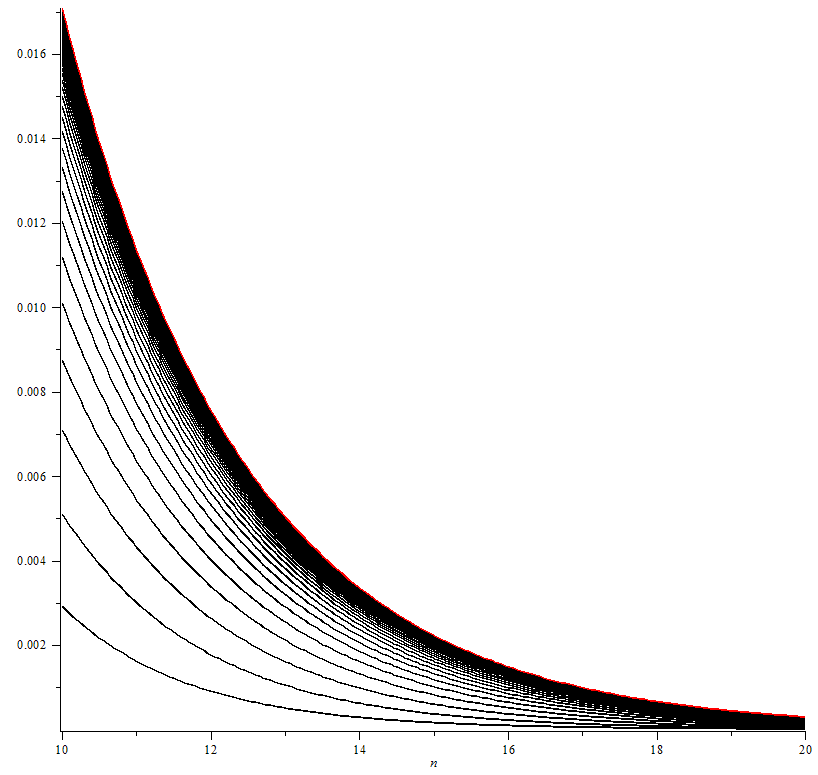
On étudie ici le comportement d’une file d’attente avec \(\lambda\) et \(\mu\) fixés lorsque \(N \rightarrow +\infty\). Cette section permet de quantifier l’écart au modèle provoqué par la restriction de la longueur de la file et étudier son comportement lorsque \(N \rightarrow +\infty\).
Le théorème 4 appliqué avec \(\omega_2\) donné par le corollaire 2 donne la suite à double entrée \(u_{N,n} = \|P_N^n – P_N^{\infty}\|\) où \(P_N^n\) représente la matrice de transition de taille \(N\) itérée \(n\) fois et \(P_N^{\infty}=\lim\limits_{k \rightarrow +\infty} P^k\).
On a alors l’expression explicite :
\[u_n = \left( 2 \sqrt{\lambda \mu} \cos\left(\frac{\pi}{N}\right)+1-\lambda-\mu\right)^n \text{.}\]
On peut ainsi faire tendre \(N\) vers \(+\infty\) uniformément par rapport à \(n\) :
\[u_{\infty,n} = ( 2 \sqrt{\lambda \mu}+1-\lambda-\mu)^n \text{.}\]
(cf figure 1 en annexe)
Expression explicite de la distribution d’équilibre
Soit \(X=(x_i)_{i \in [ 1,N ]}\) la distribution d’équilibre associée à \(P\) stochastique colonne. On a donc :
\[(1) \left\{ \begin{array}{l} P X = X \\ \sum\limits_{i=1}^N x_i = 1 \end{array} \right.\]
Soit :
\[\left\{ \begin{array}{l} Q = \left( \begin{array}{c} {}^t \! P-I \\ \hline 1 \cdots 1 \end{array} \right) \\ {} \\ Y = \left( \begin{array}{ccl} 0 \\ \vdots \\ 0 \\ 1 \end{array} \right) \end{array} \right.\]
On a alors : \((1) \Leftrightarrow Q X = Y\).
Cette équation est résoluble numériquement en temps \(\operatorname{O}(N^2)\) dans le cas général d’une chaîne de Markov admettant une unique distribution d’équilibre, mais dans le cas d’une file M/M/1, on peut calculer \(X\) explicitement à partir de \((1)\).
\[(1) \Leftrightarrow \left\{ \begin{array}{l} (1-\mu) x_1 + \lambda x_2 = x_1 \\ \forall i \in [ 1,N-2 ], \mu x_i + (1-\lambda-\mu) x_{i+1} + \lambda x_{i+2} = x_{i+1} \\ \mu x_{N-1} + (1-\lambda) x_N = x_N \end{array} \right.\]
Soit \(\rho = \frac{\mu}{\lambda}\)
On a alors :
\[(1) \Leftrightarrow \forall i \in [ 2,N ], x_i = \rho^{i-1} x_1\]
Or, la condition \(\sum\limits_{i=1}^N x_i = 1\) impose :
\[\sum\limits_{i=1}^N \rho^{i-1} x_1 = 1\]
d’où :
\[x_1 \frac{1-\rho^N}{1-\rho} = 1\]
ainsi on a :
\[x_1 = \frac{1-\rho}{1-\rho^N} \text{.}\]
On en déduit l’expression explicite de la distribution d’équilibre :
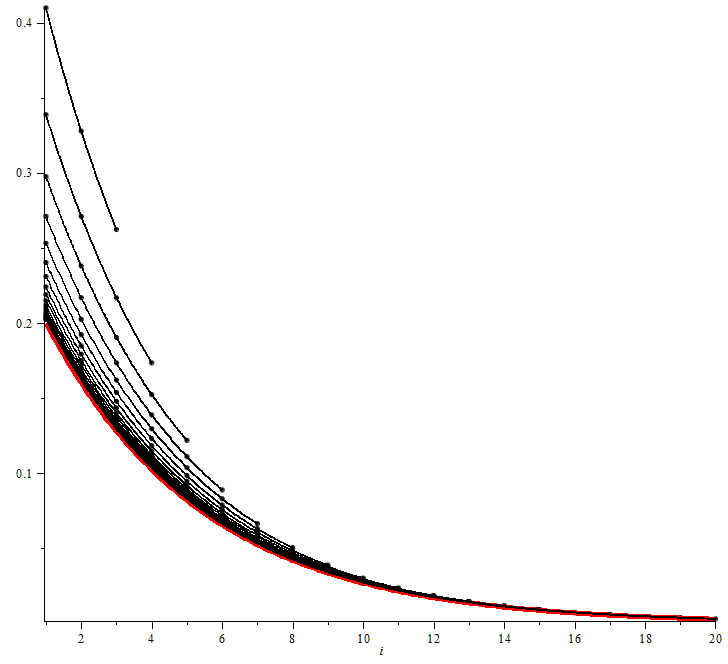
\[\forall i \in [ 1,N ], x_i = \rho^{i-1} \frac{1-\rho}{1-\rho^N} \text{.}\]
La limite correspond à une file d’attente illimitée :
\[\forall i \in \mathbb{N}^{\star}, x_i = \rho^{i-1} (1-\rho) \text{.}\]
(cf figure 2 en annexe)
On en déduit également des informations sur le comportement de la file d’attente :
- Proportion de temps libre du serveur (0 clients dans la file) : \(\frac{1-\rho}{1-\rho^N}\)
- Espérance d’attente dans la file : \(E=\sum\limits_{i=1}^{N} i \rho^{i-1} \frac{1-\rho}{1-\rho^N} \text{.}\)
Le calcul donne : \[E=\frac{\rho^{N+1}((N+1)\rho-N-1-\rho)}{\rho(\rho^N-1)(\rho-1)} + \frac{1}{(\rho^N-1)(\rho-1)}\]
Dans le cas d’une file d’attente illimitée, on obtient une espérance : \[E_{\text{file illimitée}} = \frac{1}{1-\rho}\]
L’étude des chaînes de Markov à états finis permet donc de trouver des résultats valides pour un nombre infini d’états sans passer par la théorie de la mesure.
Conclusion
Cette étude a rencontré plusieurs écueils, dont certains ont été surmontés (par exemple avant de trouver la formule explicite des valeurs propres d’une file M/M/1, j’ai essayé de contrôler les valeurs propres via des entrelacements de racines). Cependant, j’ai pu établir les théorèmes intéressants sur la convergence des files d’attente, via des résultats spectraux sur les endomorphismes symétriques, ce qui montre l’intérêt de l’algèbre linéaire dans des domaines très variés.
Annexe : illustrations
Références
[1] P. Brémaud, Markov chains, Gibbs fields, Monte Carlo simulation, and queues, Springer, 1999.
[2] A. Engel, Processus aléatoires pour les débutants, Cassini, 1976.
[3] D. Flipo, Chaînes de Markov, http://daniel.flipo.free.fr/cours/markov.pdf.
[4] J. Resing I. Adan, Queueing theory, 2002.
[5] A. W. Knapp J. G. Kemeny, J. L. Snell, Denumerable Markov chains, Springer, 1966.
[6] J. L. Snell J. G. Kemeny, Finite Markov chains, Springer, 1960.
[7] Carl D. Meyer, Matrix analysis and applied linear algebra, SIAM, 2000.
[8] D. W. Stroock, An introduction to Markov processes, Springer, 2005.
[9] S. S. Cheng W.-C. Yueh, Explicit eigenvalues and inverses of tridiagonal Toeplitz matrices with four perturbed corners, ANZIAM, 2008.
[10] W. Whitt, Continuous-time Markov chains, www.columbia.edu/~ww2040, 2006.
[11] M. Zukerman, Introduction to queuing theory and stochastic teletraffic models, http://www.ee.cityu.edu.hk/~zukerman/classnotes.pdf, 2011.
