At Hello Watt, we help residential energy consumers reduce their energy bills through various means. This involves estimating their electricity and gas consumption based on information we collect either over the phone or through a form.
Historically, this estimation was performed by a static script, based on domain knowledge that made several assumptions about the habits of our users and the environment (e.g. average outside temperature), with no way of verifying these assumptions.
Since some of our services involve getting access to precise electrical consumption load curves¹ for analysis and automated diagnostic of power use, we were presented with an opportunity of using these anonymized data to replace the previous model with a more robust and data-driven approach.
We developed Consumption Calculator, a new model that works very similarly to the previous model except its coefficients are optimized automatically based on training data derived from our database.
The inputs
This model takes as input a set of metadata fields that the user shares with us via a form. It also uses weather information that is fetched from several providers.
The model itself requires all metadata items to be known, and for training we use only homes for which this is the case. However, when the model is used to make a prediction, some of these fields can be set to a default value.
The required fields for a prediction are:
- The type of energy used for heating (electricity, gas or other)
- The habitable surface of the home in square meters
- The type of home (flat or house)
These fields can be inferred from other fields through hand-crafted heuristics if unknown:
- The number of floors in the home (which defaults to 2 for a home larger than 100 square meters, otherwise 1)
- The number of inhabitants in the home (which defaults to a number that is an affine function of the home surface)
This field has a static default value:
- The type of energy used for water heating (which defaults to electricity)
Finally, this field defaults to the average value it takes in the training set:
- coldness is computed from the daily temperature averages in the area where the home is located. We observe that people start heating their homes when the average daily outside temperature drops below 15 °C, therefore we compute coldness as the average of
max(T — 15°C, 0)over all daily temperatures. A place where the daily temperature never drops below 15 °C has a coldness of 0, otherwise the coldness is always negative.
The model
We use a parametric model, where weights are trained using gradient descent based on the daily consumptions we collected.
First, we start by computing the surface of walls and ceiling assuming the home is square, which gives us an estimate of thermal losses. Then the consumption of devices is estimated based on relevant metadata.
# ELEC
ceiling_surface = home_surface / floor_count
walls_surface = sqrt(home_surface * floor_count)
thermal_losses = w[0] * ceiling_surface + walls_surface
c_base = w[1]
c_sp = w[2] * has_swimming_pool * home_surface
c_personal = w[3] * inhabitants
c_heating = w[4] * (heating == ELEC) * (-coldness) * thermal_losses
c_wh = w[5] * (water_heating == ELEC) * inhabitants
c_total = c_base + c_sp + c_personal + c_heating + c_wh
# GAS
c_heating = v[0] * (heating == GAS) * (-coldness) * thermal_losses
c_wh = v[1] * (water_heating == GAS) * inhabitants
c_total = c_heating + c_wh
As an added bonus, we can exploit intermediate variables of the model to get an estimated consumption per device.
Extra care was taken to avoid under-constraining the model. For instance, consider the following model:
c_washing_machine = w[0] * inhabitants
c_dryer = w[1] * inhabitants
c_total = c_dryer + c_washing_machine
It can be factored to:
c_total = (w[0] + w[1]) * inhabitants
This means that many solutions have the same loss, and the optimization procedure may choose unbounded values for these parameters. This is generally a bad idea because of the limits of floating-point arithmetic, but also because it becomes very hard to assign meaning to intermediate variables of the model. If w[0] = .1 and w[1] = .2 we can say that a washing machine uses half as much power than a dryer, but what about if w[0] = -999.9 and w[1] = 1000.2 , and what about if w[0] = 0 and w[1] = .3 ? These parameters all result in the exact same model so there is no way to interpret their selection.
Training
We used an Adam optimizer for gradient descent.
As for the choice of loss function, we tried several options. Since we have a wide range of consumption, mean absolute error (MAE) and mean square error (MSE) allow very big relative errors for small consumption. Relative error (RE) tends to under-estimate consumption (RE for under-estimations cannot be more than 100%, but RE for over-estimations is unbounded). In the end we settled on Symmetric mean absolute percentage error (SMAPE) which is a variant of relative error that treats the target and prediction symmetrically, preventing any bias.
The output
The output of our model consists in the average daily energy consumption of the home. We run the models for electricity and gas independently but both energies are measured in kWh, so the main output of our model is always in kWh/day.
Using our method we are also able to obtain the contributions of heating, water heating, as well as the “constant” and the “personal” components, the latter being linear in the number of inhabitants and accounting for the usage various appliances (washing machine, dryer, dishwasher, computers, TV, etc.).
Our trained model also gives us an insight into the relative importance of each of these components, which can be expressed through its parameters.
- The trained model uses the following equation for thermal losses:
thermal_losses = 0.02 * ceiling_surface + walls_surfacesuggesting that most of the heat losses are better explained using a square-root law rather than a linear law. - Electrical water heating uses 1.36 kWh/day/person, and gas water heating 1.86/day/person.
- Our model also extracts a component that is linear in the number of inhabitants (washing machine, dryer, dishwasher, computers, TV, etc.) and a constant component (always-on devices, etc.)
Of course these numbers are approximate, they simply translate the best way to fit the metadata to the recorded consumptions. Some items have a heavy bias, for instance gas cooking is very rare which reduces the independence of some of our parameters.
Our testing tool
We set up a simple flask app to test our model and visualize the disaggregation estimates (here we only presented a simplified model, but our internal model takes into account more inputs).
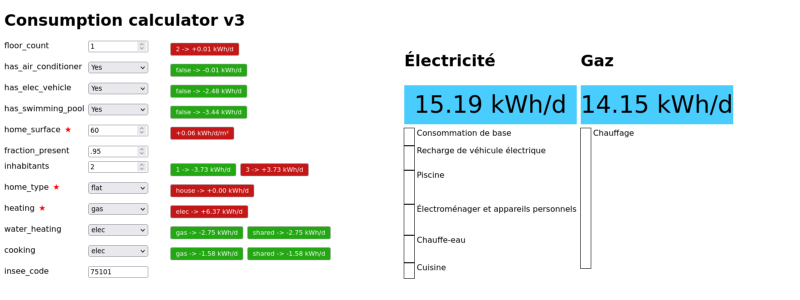
The red and green boxes indicate the marginal contribution of each metadata item to the electrical consumption (red for parameter changes that would increase consumption, and green for changes that would decrease it).
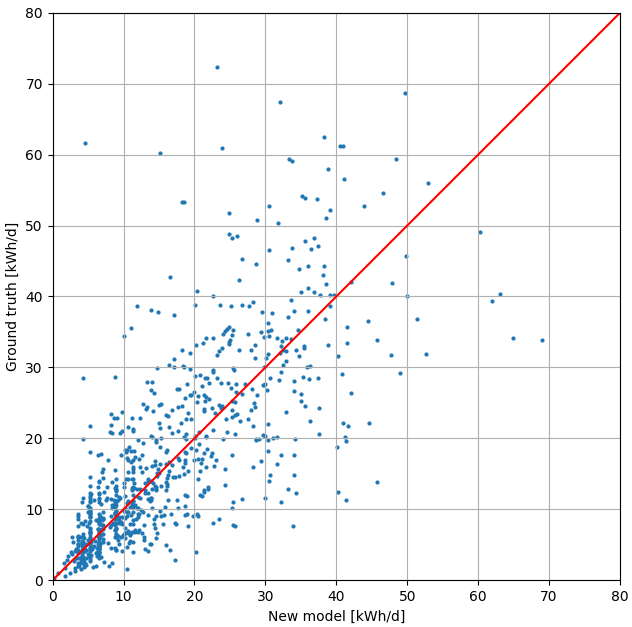
The following plot shows the prediction vs. real consumption for 1000 homes in our database, and suggests our model is well balanced.
Conclusion
This new model is gradually replacing the previous hand-crafted model, and is more precise and data-driven. It takes into account weather data which was not done in the previous model, and opens up new opportunities such as predicting the consumption for each month of the year.
The new model is going to be used throughout our company, both externally in various parts of our website, and internally in dedicated tools used by our advisors. Our web platform contains several forms that can be used by anyone to estimate their consumption, bill, and choose the best energy provider in terms of sustainability, price and popularity. Our specialized advisors also need to predict the consumption of homes to calculate the amortization rates of renovation works or the installation of solar panels.
[1] Today tens of thousands of users choose to share their consumption data with our company so that they can benefit from detailed analysis and help us improve our services.
