The problem with DDPG: understanding failures in deterministic environments with sparse rewards

Published at ICANN 2020, PDF version on arxiv

Authors: Guillaume Matheron, Nicolas Perrin, Olivier Sigaud
Sorbonne Université, CNRS, Institut des Systèmes Intelligents et de Robotique

⋆This work was partially supported by the French National Research Agency (ANR), Project ANR-18-CE33-0005 HUSKI.

In environments with continuous state and action spaces, state-of-the-art actor-critic reinforcement learning algorithms can solve very complex problems, yet can also fail in environments that seem trivial, but the reason for such failures is still poorly understood. In this paper, we contribute a formal explanation of these failures in the particular case of sparse reward and deterministic environments. First, using a very elementary control problem, we illustrate that the learning process can get stuck into a fixed point corresponding to a poor solution, especially when the reward is not found very early. Then, generalizing from the studied example, we provide a detailed analysis of the underlying mechanisms which results in a new understanding of one of the convergence regimes of these algorithms.

1 Introduction

The Deep Deterministic Policy Gradient (DDPG) algorithm [11] is one of the earliest deep Reinforcement Learning (RL) algorithms designed to operate on potentially large continuous state and action spaces with a deterministic policy, and it is still one of the most widely used. However, it is often reported that DDPG suffers from instability in the form of sensitivity to hyper-parameters and propensity to converge to very poor solutions or even diverge. Various algorithms have improved stability by addressing well identified issues, such as the over-estimation bias in TD3 [7] but, because a fundamental understanding of the phenomena underlying these instabilities is still missing, it is unclear whether these ad hoc remedies truly address the source of the problem. Thus, better understanding why these algorithms can fail even in very simple environments is a pressing question.

To investigate this question, we introduce in Sect. 4 a very simple one-dimensional environment with a sparse reward function in which DDPG sometimes fails. Analyzing this example allows us to provide a detailed account of these failures. We then reveal the existence of a cycle of mechanisms operating in the sparse reward and deterministic case, leading to the quick convergence to a poor policy. In particular, we show that when the reward is not discovered early enough, these mechanisms can lead to a deadlock situation where neither the actor nor the critic can evolve anymore. Critically, this deadlock persists even when the agent is subsequently trained with rewarded samples.

The study of these mechanisms is backed-up with formal analyses in a simplified context where the effects of function approximation is ignored. Nevertheless, the resulting understanding helps analyzing the practical phenomena encountered when using actors and critics represented as neural networks.

Issues when combining RL with function approximation have been studied for a long time [3, 4, 17]. In particular, it is well known that deep RL algorithms can diverge when they meet three conditions coined as the ”deadly triad” [16], that is when they use (1) function approximation, (2) bootstrapping updates and (3) off-policy learning. However, these questions are mostly studied in the continuous state, discrete action case. For instance, several recent papers have studied the mechanism of this instability using DQN [12]. In this context, four failure modes have been identified from a theoretical point of view by considering the effect of a linear approximation of the deep-Q updates and by identifying conditions under which the approximate updates of the critic are contraction maps for some distance over Q-functions [1]. Meanwhile, [10] shows that, due to its stabilizing heuristics, DQN does not diverge much in practice when applied to the atari domain.

In contrast to these papers, here we study a failure mode specific to continuous action actor-critic algorithms. It hinges on the fact that one cannot take the maximum over actions, and must rely on the actor as a proxy for providing the optimal action instead. Therefore, the failure mode identified in this paper cannot be reduced to any of the ones that affect DQN. Besides, the formal analyses presented in this article show that the failure mode we are investigating does not depend on function approximation errors, thus it cannot be directly related to the deadly triad.

More related to our work, several papers have studied failure to gather rewarded experience from the environment due to poor exploration [5, 6, 14], but we go beyond this issue by studying a case where the reward is actually found but not properly exploited. Finally, like us the authors of [8] study a failure mode which is specific to DDPG-like algorithms, but the studied failure mode is different. They show under a batch learning regime that DDPG suffers from an extrapolation error phenomenon, whereas we are in the more standard incremental learning setting and focus on a deadlock resulting from the shape of the Q-function in the sparse reward case.

3 Background: Deep Deterministic Policy Gradient

The DDPG algorithm [11] is a deep RL algorithm based on the Deterministic Policy Gradient theorem [15]. It borrows the use of a replay buffer and target networks from DQN [13]. DDPG is an instance of the Actor-Critic model. It learns both an actor function $\pi _\psi $ (also called policy) and a critic function $Q_\theta $, represented as neural networks whose parameters are respectively noted $\psi $ and $\theta $.

The deterministic actor takes a state $s \in S$ as input and outputs an action $a \in A$. The critic maps each state-action pair $(s,a)$ to a value in $\mathbb {R}$. The reward $r: S \times A \rightarrow \mathbb {R}$, the termination function $t: S \times A \rightarrow \{0,1\}$ and the discount factor $\gamma < 1$ are also specified as part of the environment.

The actor and critic are updated using stochastic gradient descent on two losses $L_{\psi }$ and $L_{\theta }$. These losses are computed from mini-batches of samples $(s_i, a_i, r_i, t_i, s_{i+1})$, where each sample corresponds to a transition $s_i \rightarrow s_{i+1}$ resulting from performing action $a_i$ in state $s_i$, with subsequent reward $r_i = r(s_i, a_i)$ and termination index $t_i = t(s_i, a_i)$.

Two target networks $\pi _{\psi ‘}$ and $Q_{\theta ‘}$ are also used in DDPG. Their parameters $\psi ‘$ and $\theta ‘$ respectively track $\psi $ and $\theta $ using exponential smoothing. They are mostly useful to stabilize function approximation when learning the critic and actor networks. Since they do not play a significant role in the phenomena studied in this paper, we ignore them in our formal analyses.

Equations \eqref{eq:ddpg_actor} and \eqref{eq:ddpg_critic} define $L_{\psi }$ and $L_{\theta }$:

$$ \begin{equation}\tag{1}\label{eq:ddpg_actor} L_{\psi } = – \sum _i Q_\theta \left ( s_i, \pi _\psi \left (s_i\right )\right ) \end{equation}$$

$$\begin{equation}\left \{\begin {aligned} \forall i, y_i & = r_i + \gamma (1-t_i) Q_{\theta ‘}\left (s_{i+1}, \pi _{\psi ‘}\left (s_{i+1}\right )\right ) \\ L_{\theta } &= \sum _i \Big [ Q_\theta \left (s_i,a_i\right ) – y_i \Big ]^2\text {.} \end {aligned}\right .\end{equation} \tag{2}\label{eq:ddpg_critic} $$

Training for the loss given in \eqref{eq:ddpg_actor} yields the parameter update in \eqref{eq:update_actor}, with $\alpha $ the learning rate:

$$ \begin{equation} \psi \leftarrow \psi + \alpha \sum _i \frac {\partial \pi _\psi (s_i)}{\partial \psi }^T \left .\nabla _a Q_{\theta }(s_i, a)\right |_{a=\pi _\psi (s_i)}. \tag{3}\label{eq:update_actor}\end{equation}$$

As DDPG uses a replay buffer, the mini-batch samples are acquired using a behavior policy $\beta $ which may be different from the actor $\pi $. Usually, $\beta $ is defined as $\pi $ plus a noise distribution, which in the case of DDPG is either a Gaussian function or the more sophisticated Ornstein-Uhlenbeck noise.

Importantly for this paper, the behavior of DDPG can be characterized as an intermediate between two extreme regimes:

When the actor is updated much faster than the critic, the policy becomes greedy with respect to this critic, resulting into a behavior closely resembling that of the Q-Learning algorithm. When it is close to this regime, DDPG can be characterized as off-policy.
When the critic is updated much faster than the actor, the critic tends towards $Q^\pi (s, a)$. The problems studied in this paper directly come from this second regime.

4 A new failure mode

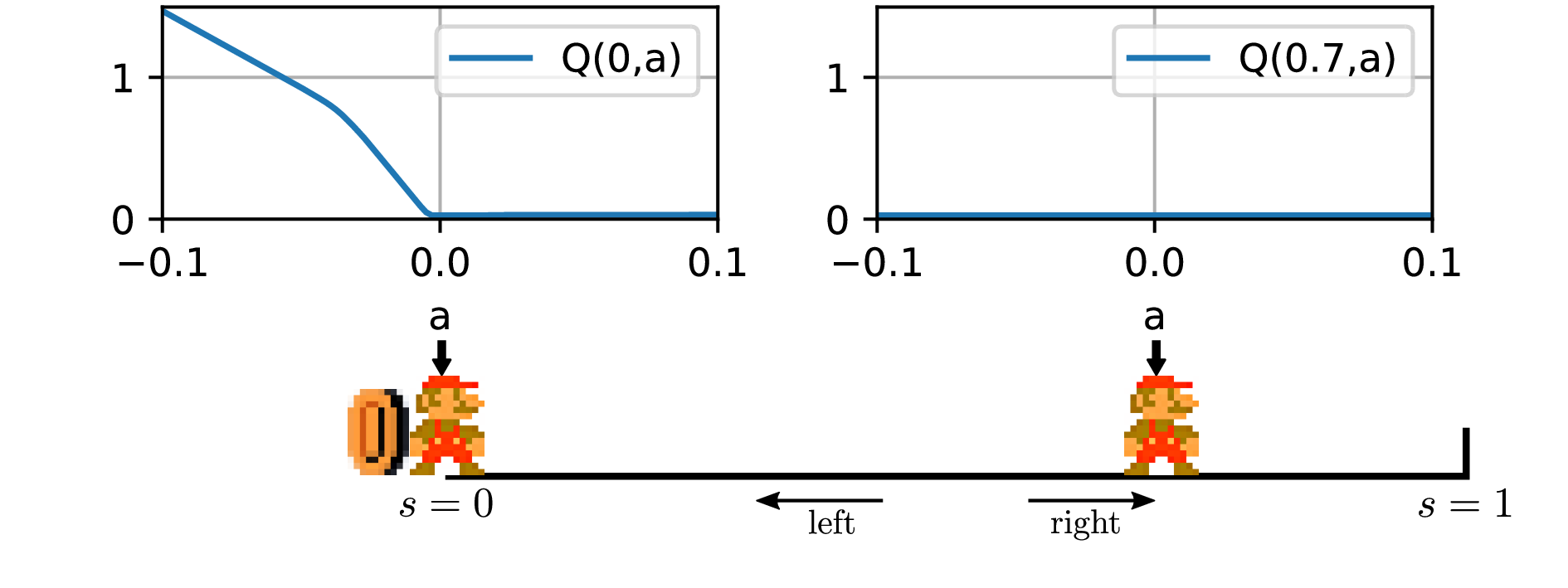
In this section, we introduce a simplistic environment which we call 1D-toy. It is a one-dimensional, discrete-time, continuous state and action problem, depicted in Fig. 1.

$$\begin {align} S &= [0, 1] \\ A &= [-0.1, 0.1]\\ s_0 &= 0\\ s_{t+1} &= \min \left (1, \max \left (0, s_t + a_t\right )\right ) \\ r_{t} &= t_{t} = \mathbb {1}_{s_t + a_t < 0} \end {align} $$

Despite its simplicity, DDPG can fail on 1D-toy. We first show that DDPG fails to reach $100\%$ success. We then show that if learning a policy does not succeed soon enough, the learning process can get stuck. Besides, we show that the initial actor can be significantly modified in the initial stages before finding the first reward. We explain how the combination of these phenomena can result into a deadlock situation. We generalize this explanation to any deterministic and sparse reward environment by revealing and formally studying a undesirable cyclic process which arises in such cases. Finally, we explore the consequences of getting into this cyclic process.

4.1 Empirical study

In all experiments, we set the maximum episode length $N$ to $50$, but the observed phenomena persist with other values.

Residual failure to converge using different noise processes. We start by running DDPG on the 1D-toy environment. This environment is trivial as one infinitesimal step to the left is enough to obtain the reward, end the episode and succeed, thus we might expect a quick $100\%$ success. However, the first attempt using an Ornstein-Uhlenbeck (OU) noise process shows that DDPG succeeds in only 94% of cases, see Fig. 2a.

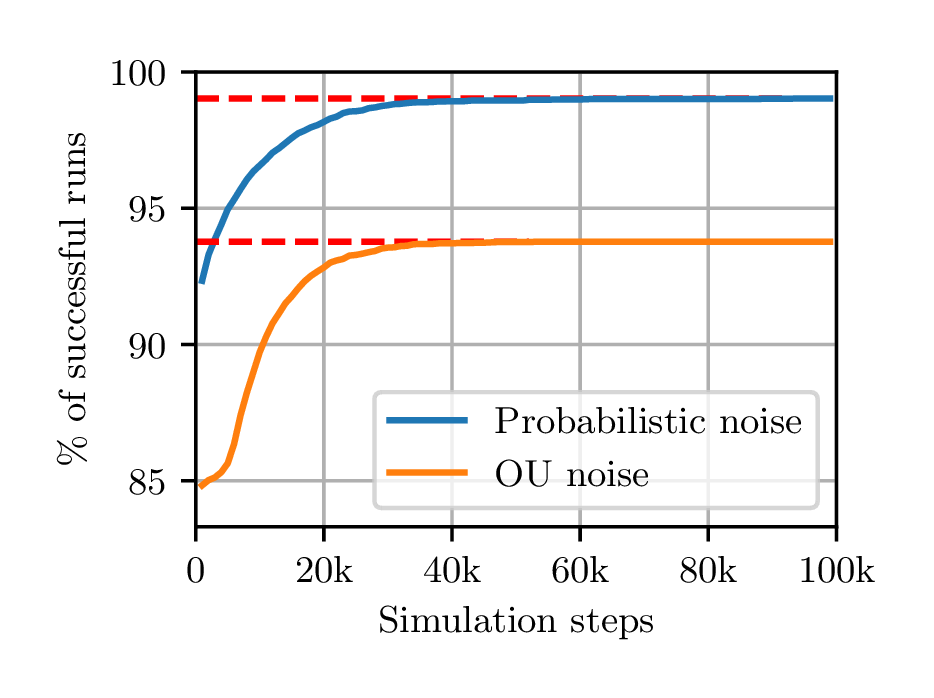
**Fig. 2a:** Success rate of DDPG with Ornstein-Uhlenbeck (OU) and probabilistic noise. Even with probabilistic noise, DDPG fails on about 1% of the seeds.

**Fig. 2b:** Comparison between DDPG with probabilistic noise and a variant in which the behavior policy is set to the optimal policy $\pi ^*$ after 20k steps.

These failures might come from an exploration problem. Indeed, at the start of each episode the OU noise process is reset to zero and gives little noise in the first steps of the episode. In order to remove this potential source of failure, we replace the OU noise process with an exploration strategy similar to $\epsilon $-greedy which we call ”probabilistic noise”. For some $0<p<1$, with probability $p$, the action is randomly sampled (and the actor is ignored), and with probability $1-p$ no noise is used and the raw action is returned. In our tests, we used $p=0.1$. This guarantees at least a 5% chance of success at the first step of each episode, for any policy. Nevertheless, Fig. 2a shows that even with probabilistic noise, about $1\%$ of seeds still fail to converge to a successful policy in 1D-toy, even after 100k training steps. All the following tests are performed using probabilistic noise.

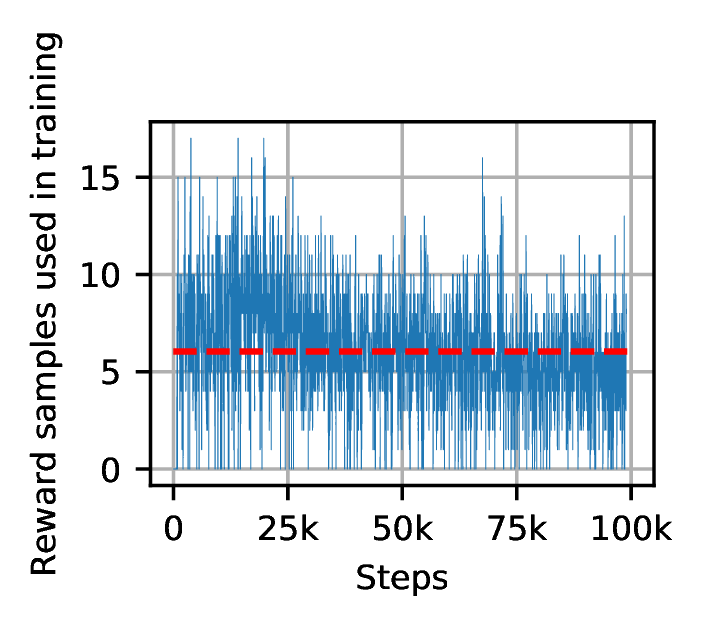
We now focus on these failures. On all failing seeds, we observe that the actor has converged to a saturated policy that always goes to the right ($\forall s, \pi (s)=0.1$). However, some mini-batch samples have non-zero rewards because the agent still occasionally moves to the left, due to the probabilistic noise applied during rollouts. The expected fraction of non-zero rewards is slightly more than 0.1%¹ . Fig. 3a shows the occurrence of rewards in minibatches taken from the replay buffer when training DDPG on 1D-toy. After each rollout (episode) of $n$ steps, the critic and actor networks are trained $n$ times on minibatches of size 100. So for instance, a failed episode of size 50 is followed by a training on a total of 5000 samples, out of which we expect more than 5 in average are rewarded transitions.

The constant presence of rewarded transitions in the minibatches suggests that the failures of DDPG on this environment are not due to insufficient exploration by the behavior policy.

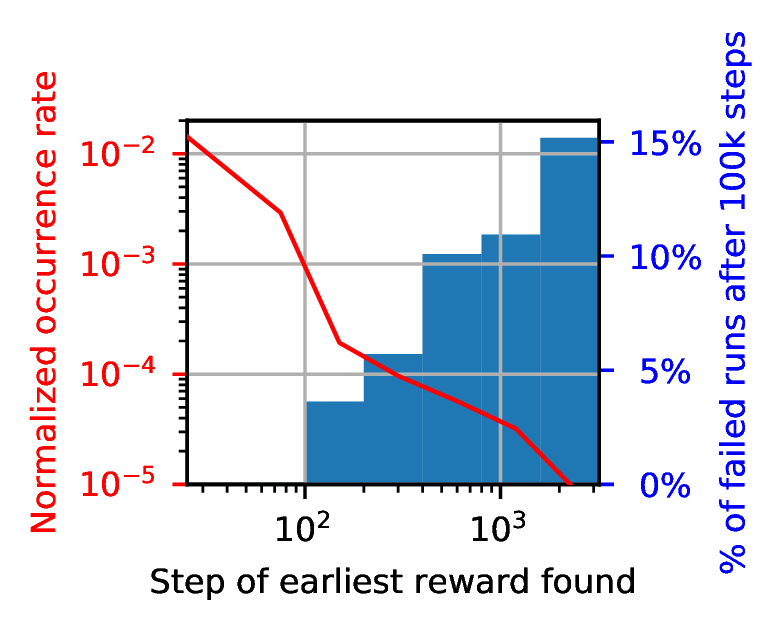
**Fig. 3a:** Number of rewards found in mini-batches during training. After a rollout of $n$ steps, the actor and critic are both trained on $n$ minibatches of size 100. The red dotted line indicates an average of 6.03 rewarded transitions present in these $n$ minibatches.

**Fig. 3b:** In red, normalized probability of finding the earliest reward at this step. In blue, for each earliest reward bin, fraction of these episodes that fail to converge to a good actor after 100k steps. Note that when the reward is found after one or two episodes, the convergence to a successful actor is certain.

Correlation between finding the reward early and finding the optimal policy. We have shown that DDPG can get stuck in 1D-toy despite finding the reward regularly. Now we show that when DDPG finds the reward early in the training session, it is also more successful in converging to the optimal policy. On the other hand, when the first reward is found late, the learning process more often gets stuck with a sub-optimal policy.

From Fig. 3b, the early steps appear to have a high influence on whether the training will be successful or not. For instance, if the reward is found in the first 50 steps by the actor noise (which happens in 63% of cases), then the success rate of DDPG is 100%. However, if the reward is first found after more than 50 steps, then the success rate drops to 96%. Fig. 3b shows that finding the reward later results in lower success rates, down to 87% for runs in which the reward was not found in the first 1600 steps. Therefore, we claim that there exists a critical time frame for finding the reward in the very early stages of training.

Spontaneous actor drift. At the beginning of each training session, the actor and critic of DDPG are initialized to represent respectively close-to-zero state-action values and close-to-zero actions. Besides, as long as the agent does not find a reward, it does not benefit from any utility gradient. Thus we might expect that the actor and critic remain constant until the first reward is found. Actually, we show that even in the absence of reward, training the actor and critic triggers non-negligible updates that cause the actor to reach a saturated state very quickly.

To investigate this, we use a variant of 1D-toy called Drift where the only difference is that no rewarded or terminal transitions are present in the environment. We also use a stripped-down version of DDPG, removing rollouts and using random sampling of states and actions as minibatches for training.

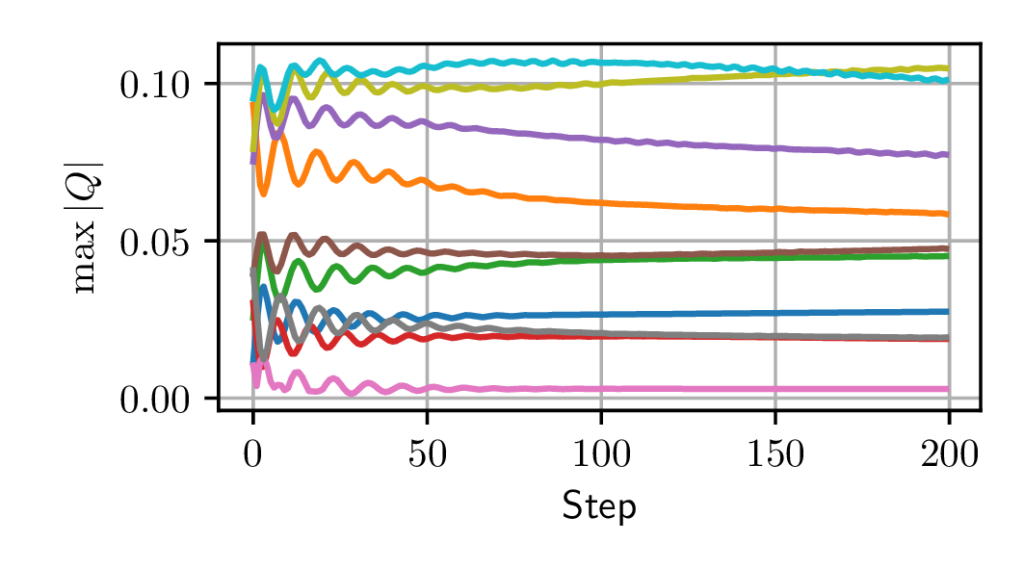
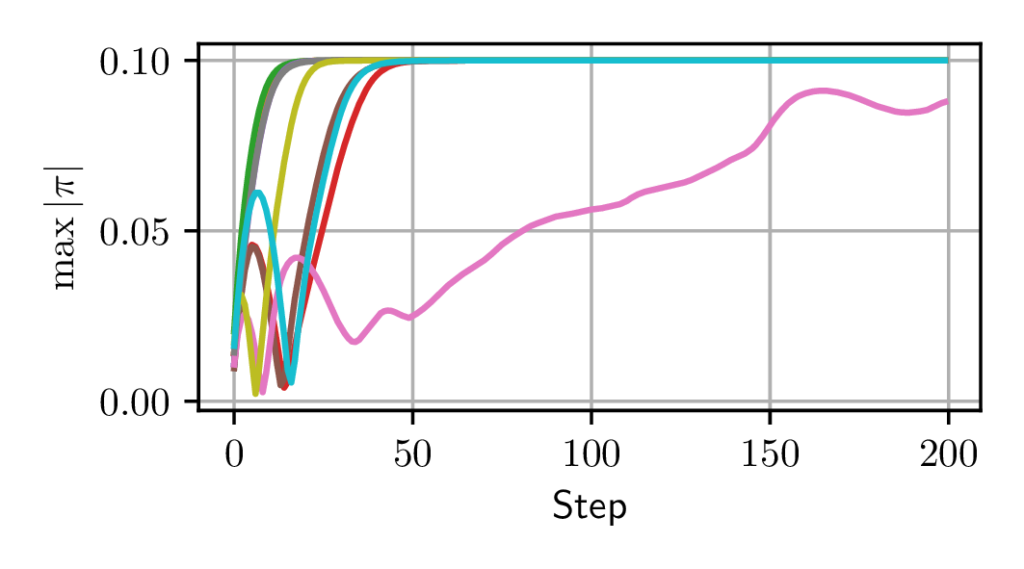
**Fig. 4a:** Drift of $\max |Q|$ (left) and $\max |\pi |$ (right) in the Drift environment, for 10 different seeds. In the absence of reward, the critic oscillates briefly before stabilizing. However, the actor very quickly reaches a saturated state, at either $\forall s, \pi (s)=0.1$ or $-0.1$.

Fig. 4b shows that even in the absence of reward, the actor function drifts rapidly (notice the horizontal scale in steps) to a saturated policy, in a number of steps comparable to the ”critical time frame” identified above. The critic also has a transitive phase before stabilizing.

In Fig. 4a, the fact that $\max _{s,a} \left |Q(s,a)\right |$ can increase in the absence of reward can seem counter-intuitive, since in the loss function presented in Equation \eqref{eq:ddpg_critic}, $\left |y_i\right |$ can never be greater than $\max _{s,a} \left |Q(s,a)\right |$. However, it should be noted that the changes made to $Q$ are not local to the minibatch points, and increasing the value of $Q$ for one input $(s,a)$ may cause its value to increase for other inputs too, which may cause an increase in the global maximum of $Q$. This phenomenon is at the heart of the over-estimation bias when learning a critic [7], but this bias does not play a key role here.

4.2 Explaining the deadlock situation for DDPG on 1D-toy

**Fig. 5a:** Critic values in the deadlock configuration. The critic is non-zero only in the region that immediately leads to a reward ($s+a<0$)

**Fig. 5b:** Two snapshots of the critic for different states in a failed run. The high $Q$ values in the $s+a<0$ region are not propagated.

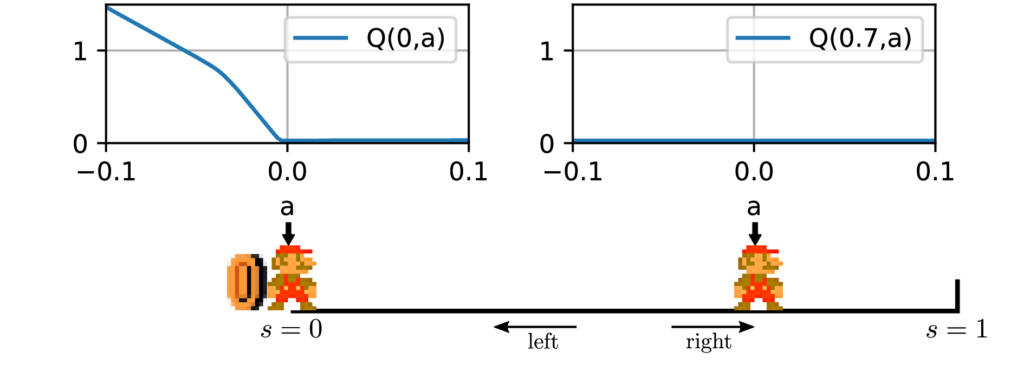
Up to now, we have shown that DDPG fails about $1\%$ of times on 1D-toy, despite the simplicity of this environment. We have now collected the necessary elements to explain the mechanisms of this deadlock in 1D-toy.

Fig. 5 shows the value of the critic in a failed run of DDPG on 1D-toy. We see that the value of the reward is not propagated correctly outside of the region in which the reward is found in a single step $\left \{(s,a)\mid s+a<0\right \}$. The key of the deadlock is that once the actor has drifted to $\forall s, \pi (s)=0.1$, it is updated according to $\left .\nabla _a Q_{\theta }(s, a)\right |_{a=\pi _\psi (s)}$ (Equation \eqref{eq:update_actor}). Fig. 5b shows that for $a=\pi (s)=0.1$, this gradient is zero therefore the actor is not updated. Besides, the critic is updated using $y_i = r(s_i,a_i) + \gamma Q(s_i’,\pi (s_i’))$ as a target. Since $Q(s_i’,0.1)$ is zero, the critic only needs to be non-zero for directly rewarded actions, and for all other samples the target value remains zero. In this state the critic loss given in Equation \ref{eq:ddpg_critic} is minimal, so there is no further update of the critic and no further propagation of the state-action values. The combination of the above two facts clearly results in a deadlock.

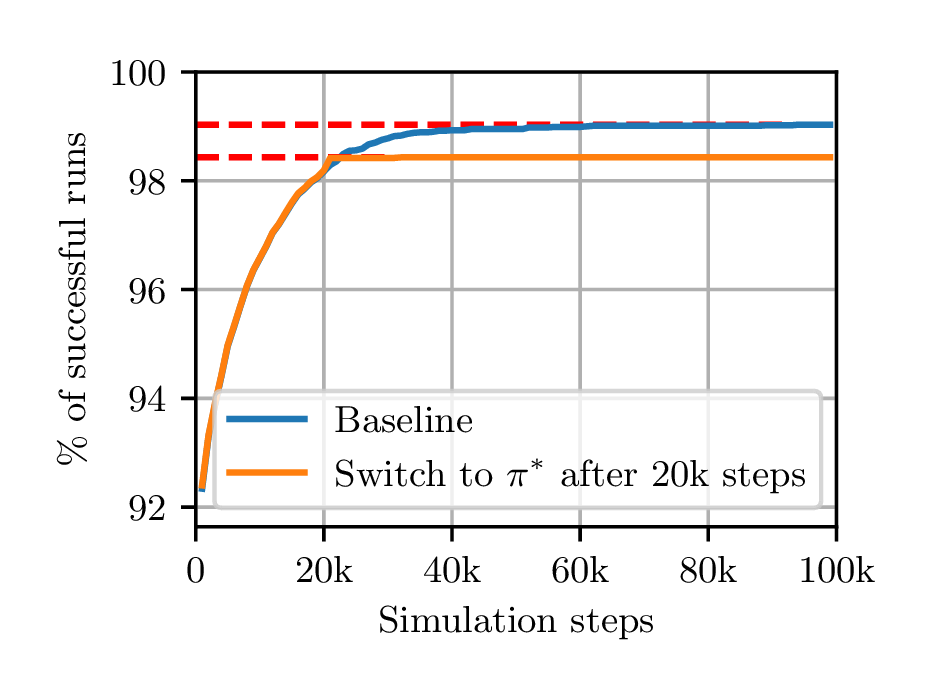
Importantly, the constitutive elements of this deadlock do not depend on the batches used to perform the update, and therefore do not depend on the experience selection method. We tested this experimentally by substituting the behavior policy for the optimal policy after 20k training steps. Results are presented in Fig. 2b and show that, once stuck, even when it is given ideal samples, DDPG stays stuck in the deadlock configuration. This also explains why finding the reward early results in better performance. When the reward is found early enough, $\pi (s_0)$ has not drifted too far, and the gradient of $Q(s_0,a)$ at $a = \pi (s_0)$ drives the actor back into the correct direction.

Note however that even when the actor drifts to the right, DDPG does not always fail. Indeed, because of function approximators the shape of the critic when finding the reward for the first time varies, and sometimes converges slowly enough for the actor to be updated before the convergence of the critic.

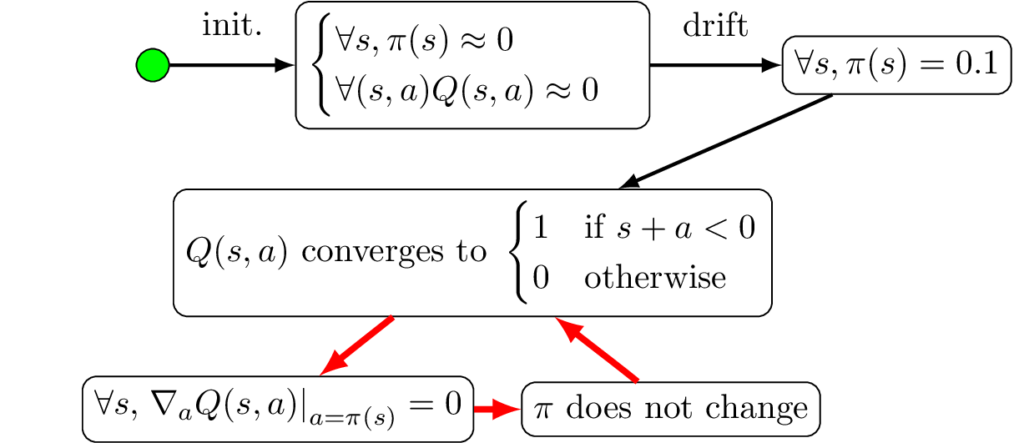
Fig. 6: Deadlock observed in 1D-toy, represented as the cycle of red arrows.

Fig. 6 summarizes the above process. The entry point is represented using a green dot. First, the actor drifts to $\forall s, \pi (s)=0.1$, then the critic converges to $Q^\pi $ which is a piecewise-constant function, which in turn means that the critic provides no gradient, therefore the actor is not updated (as seen in Equation \eqref{eq:ddpg_critic}).

4.3 Generalization

Our study of 1D-toy revealed how DDPG can get stuck in this simplistic environment. We now generalize to the broader context of more general continuous action actor critic algorithms, including at least DDPG and TD3, and acting in any deterministic and sparse reward environment. The generalized deadlock mechanism is illustrated in Fig. 7 and explained hereafter in the idealized context of perfect approximators.

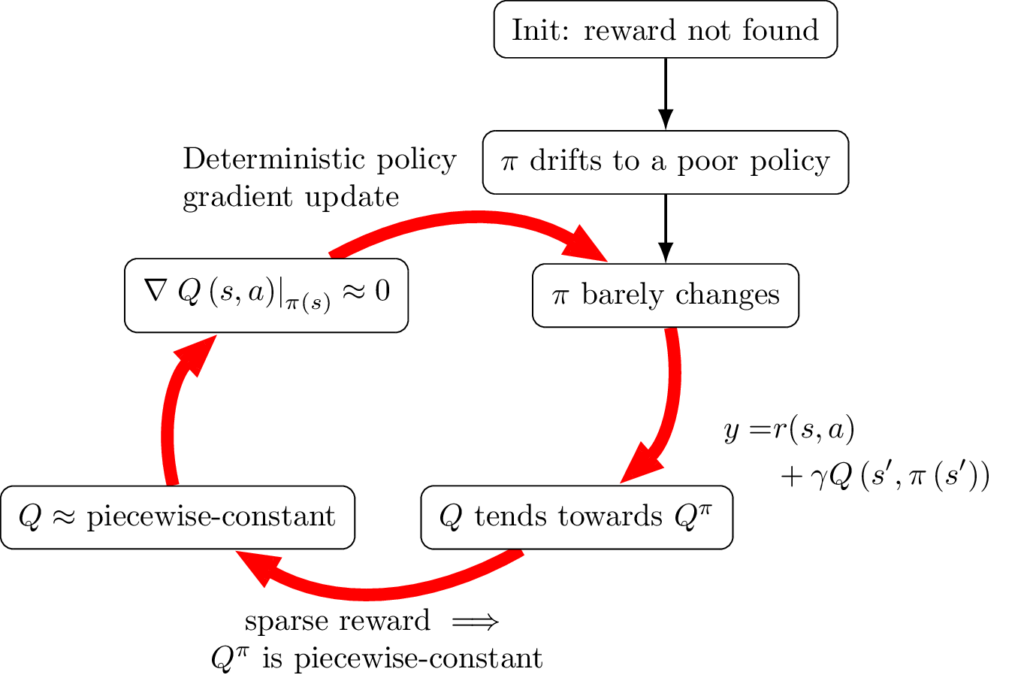
Fig. 7: A cyclic view of the undesirable convergence process in continuous action actor-critic algorithms, in the deterministic and sparse reward case.

Entry point: As shown in the previous section, before the behavior policy finds any reward, training the actor and critic can still trigger non-negligible updates that may cause the actor to quickly reach a poor state and stabilize. This defines our entry point in the process.

$\mathbf {Q}$ tends towards $\mathbf {Q^{\boldsymbol {\pi }}}$: A first step into the cycle is that, if the critic is updated faster than the policy, the update rule of the critic $Q$ given in Equation \eqref{eq:ddpg_critic} makes $Q$ converge to $Q^\pi $. Indeed, if $\pi $ is fixed, $Q$ is updated regularly via approximate dynamic programming with the Bellman operator for the policy $\pi $. Under strong assumptions, or assuming exact dynamic programming, it is possible to prove that the iterated application of this operator converges towards a unique function $Q^\pi $, which corresponds to the state-action value function of $\pi $ as defined above [9].

$\mathbf {Q^{\boldsymbol {\pi }}}$ is piecewise-constant: In a deterministic environment with sparse terminal rewards, $Q^\pi $ is piecewise-constant because $V^\pi (s’)$ only depends on two things: the (integer) number of steps required to reach a rewarded state from $s’$, and the value of this reward state, which is itself piecewise-constant. Note that we can reach the same conclusion with non-terminal rewards, by making the stronger hypothesis on the actor that $\forall s, r(s,\pi (s))=0$. Notably, this is the case for the actor $\forall s, \pi (s)=0.1$ on 1D-toy.

Q is approximately piecewise-constant and $\mathbf {\left .\nabla _a Q(s,a)\right |_{a=\pi (s)} \approx 0}$: Quite obviously, from $Q^\pi $ is piecewise-constant and $Q$ tends towards $Q^\pi $, we can infer that $Q$ progressively becomes almost piecewise-constant as the cyclic process unfolds. Actually, the $Q$ function is estimated by a function approximator which is never truly discontinuous. The impact of this fact is studied in Sect. 4.5. However, we can expect $Q$ to have mostly flat gradients since it is trained to match a piecewise-constant function. We can thus infer that, globally, $\left .\nabla _a Q(s,a)\right |_{a=\pi (s)} \approx 0$. And critically, the gradients in the flat regions far from the discontinuities give little information as to how to reach regions of higher values.

$\boldsymbol {\pi }$ barely changes: DDPG uses the deterministic policy gradient update, as seen in Equation \ref{eq:update_actor}. This is an analytical gradient that does not incorporate any stochasticity, because $Q$ is always differentiated exactly at $(s,\pi (s))$. Thus the actor update is stalled, even when the reward is regularly found by the behavior policy. This closes the loop of our process.

4.4 Consequences of the convergence cycle

As illustrated with the red arrows in Fig. 7, the more loops performed in the convergence process, the more the critic tends to be piecewise-constant and the less the actor tends to change. Importantly, this cyclic convergence process is triggered as soon as the changes on the policy drastically slow down or stop. What matters for the final performance is the quality of the policy reached before this convergence loop is triggered. Quite obviously, if the loop is triggered before the policy gets consistently rewarded, the final performance is deemed to be poor.

The key of this undesirable convergence cycle lies in the use of the deterministic policy gradient update given in Equation \ref{eq:update_actor}. Actually, rewarded samples found by the exploratory behavior policy $\beta $ tend to be ignored by the conjunction of two reasons. First, the critic is updated using $Q(s’,\pi (s’))$ and not $Q(s,\beta (s))$, thus if $\pi $ differs too much from $\beta $, the values brought by $\beta $ are not properly propagated. Second, the actor being updated through \eqref{eq:update_actor}, i.e. using the analytical gradient of the critic with respect to the actions of $\pi $, there is no room for considering other actions than that of $\pi $. Besides, the actor update involves only the state $s$ of the sample taken from the replay buffer, and not the reward found from this sample $r(s,a)$ or the action performed. For each sample state $s$, the actor update is intended to make $\pi (s)$ converge to $\arg\!\max _a \pi (s,a)$ but the experience of different actions performed for identical or similar states is only available through $Q(s,\cdot )$, and in DDPG it is only exploited through the gradient of $Q(s,\cdot )$ at $\pi (s)$, so the process can easily get stuck in a local optimum, especially if the critic tends towards a piecewise-constant function, which as we have shown happens when the reward is sparse. Besides, since TD3 also updates the actor according to \eqref{eq:update_actor} and the critic according to \eqref{eq:ddpg_critic}, it is susceptible to the same failures as DDPG.

4.5 Impact of function approximation

We have just explained that when the actor has drifted to an incorrect policy before finding the reward, an undesirable convergence process should result in DDPG getting stuck to this policy. However, in 1D-toy, we measured that the actor drifts to a policy moving to the right in $50\%$ of cases, but the learning process only fails $1\%$ of times. More generally, despite the issues discussed in this paper, DDPG has been shown to be efficient in many problems. This better-than-predicted success can be attributed to the impact of function approximation.

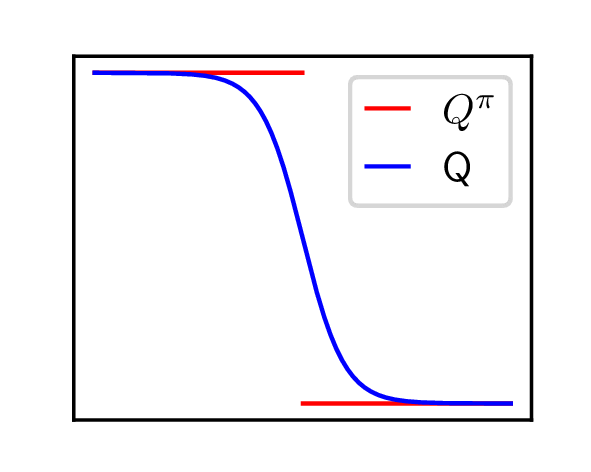
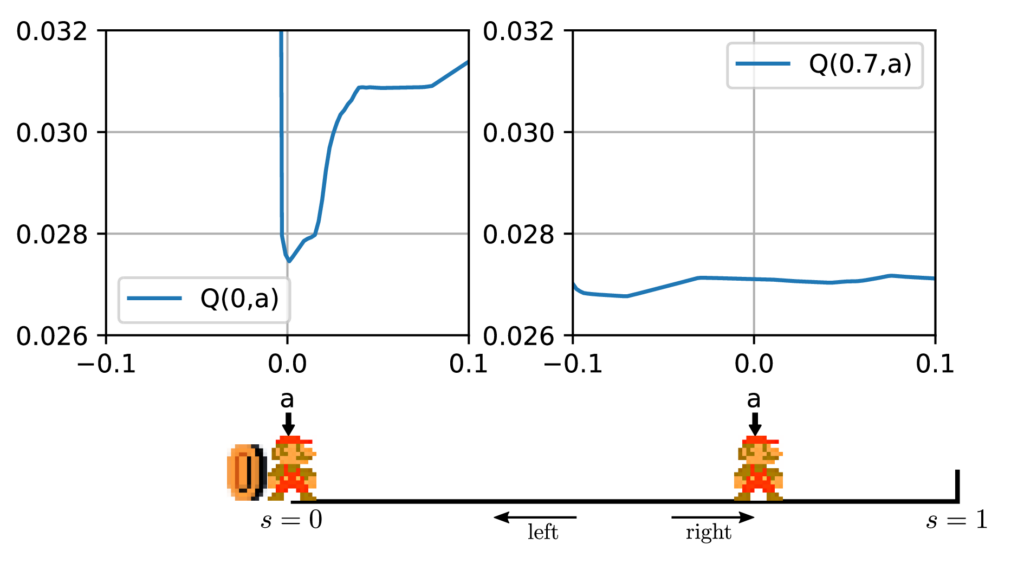
**Fig. 8a:** Example of a monotonous function approximator.

**Fig. 8b:** Simply changing the vertical scale of the graphs presented in Fig. 5b reveals that the function approximator is not perfectly flat, and has many unwanted local extrema. Specifically, continuously moving from $\pi (0)=0.1$ to $\pi (0)<0$ requires crossing a significant valley in $Q(0,a)$, while $\pi (0)=0.1$ is a strong local maximum.

Fig. 8a shows a case in which the critic approximates $Q^\pi $ while keeping a monotonous slope between the current policy value and the reward. In this case, the actor is correctly updated towards the reward (if it is close enough to the discontinuity). This is the most often observed case, and naturally we expect approximators to smooth out discontinuities in target functions in a monotonous way, which facilitates gradient ascent. However, the critic is updated not only in state-action pairs where $Q^\pi (s,a)$ is positive, but also at points where $Q^\pi (s,a)=0$, which means that the bottom part of the curve also tends to flatten. As this happens, we can imagine phenomena that are common when trying to approximate discontinuous functions, such as the overshoot observed in Fig. 8b. In this case, the gradient prevents the actor from improving.

5 Conclusion and future work

In RL, continuous action and sparse reward environments are challenging. In these environments, the fact that a good policy cannot be learned if exploration is not efficient enough to find the reward is well-known and trivial. In this paper, we have established the less trivial fact that, if exploration does find the reward consistently but not early enough, an actor-critic algorithm can get stuck into a configuration from which rewarded samples are just ignored. We have formally characterized the reasons for this situation, and we believe our work sheds new light on the convergence regime of actor-critic algorithms.

Our study was mainly built on a simplistic benchmark which made it possible to study the revealed deadlock situation in isolation from other potential failure modes such as exploration issues, the over-estimation bias, extrapolation error or the deadly triad. The impact of this deadlock situation in more complex environments is a pressing question. For this, we need to sort out and quantify the impact of these different failure modes. Using new tools such as the ones provided in [2], recent analyses of the deadly triad such as [1] as well as simple, easily visualized benchmarks and our own tools, for future work we aim to conduct deeper and more exhaustive analysis of all the instability factors of DDPG-like algorithms, with the hope to contribute in fixing them.

References

1. Achiam, J., Knight, E., Abbeel, P.: Towards Characterizing Divergence in Deep Q-Learning. arXiv:1903.08894 (2019)

2. Ahmed, Z., Roux, N.L., Norouzi, M., Schuurmans, D.: Understanding the impact of entropy on policy optimization. arXiv:1811.11214 (2019)

3. Baird, L.C., Klopf, A.H.: Technical Report WL-TR-93-1147. Wright-Patterson AIr Force Base, Ohio, Wright Laboratory (1993)

4. Boyan, J.A., Moore, A.W.: Generalization in reinforcement learning: Safely approximating the value function. In: Advances in neural information processing systems. pp. 369–376 (1995)

5. Colas, C., Sigaud, O., Oudeyer, P.Y.: GEP-PG: Decoupling Exploration and Exploitation in Deep Reinforcement Learning Algorithms. arXiv:1802.05054 (2018)

6. Fortunato, M., Azar, M.G., Piot, B., Menick, J., Osband, I., Graves, A., Mnih, V., Munos, R., Hassabis, D., Pietquin, O., Blundell, C., Legg, S.: Noisy Networks for Exploration. arXiv:1706.10295 (2017)

7. Fujimoto, S., Hoof, H.v., Meger, D.: Addressing Function Approximation Error in Actor-Critic Methods. ICML (2018)

8. Fujimoto, S., Meger, D., Precup, D.: Off-Policy Deep Reinforcement Learning without Exploration. arXiv:1812.02900 (2018)

9. Geist, M., Pietquin, O.: Parametric value function approximation: A unified view. In: ADPRL 2011. pp. 9–16. Paris, France (2011)

10. van Hasselt, H., Doron, Y., Strub, F., Hessel, M., Sonnerat, N., Modayil, J.: Deep Reinforcement Learning and the Deadly Triad. arXiv:1812.02648 (2018)

11. Lillicrap, T.P., Hunt, J.J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., Silver, D., Wierstra, D.: Continuous control with deep reinforcement learning. arXiv:1509.02971 (2015)

12. Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., Riedmiller, M.: Playing Atari with Deep Reinforcement Learning. arXiv:1312.5602 (2013)

13. Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A.A., Veness, J., Bellemare, M.G., Graves, A., Riedmiller, M., Fidjeland, A.K., Ostrovski, G., Petersen, S., Beattie, C., Sadik, A., Antonoglou, I., King, H., Kumaran, D., Wierstra, D., Legg, S., Hassabis, D.: Human-level control through deep reinforcement learning. Nature 518(7540), 529–533 (2015)

14. Plappert, M., Houthooft, R., Dhariwal, P., Sidor, S., Chen, R.Y., Chen, X., Asfour, T., Abbeel, P., Andrychowicz, M.: Parameter space noise for exploration. arXiv preprint arXiv:1706.01905 (2017)

15. Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., Riedmiller, M.: Deterministic Policy Gradient Algorithms. In: International Conference on Machine Learning. pp. 387–395 (2014)

16. Sutton, R.S., Barto, A.G.: Reinforcement Learning: An Introduction. MIT Press (2018)

17. Tsitsiklis, J.N., Van Roy, B.: Analysis of temporal-diffference learning with function approximation. In: Advances in neural information processing systems. pp. 1075–1081 (1997)